3. Multilayer perceptron & Forward Pass

Motivation

• 이전의 Single Layer Perceptron 같은 경우 XOR Problem와 같은 Non-linear한 데이터들에 대해서는 유연하게 대처하지 못했다.

• 즉, 이렇듯 2개의 결과를 내기 위해서는 한 개의 퍼셉트론이 아닌 여러 개의 퍼셉트론이 필요하다를 의미 ⇒ 그러면, 여러 개의 Input에 대해 여러 개의 node를 타는 것이 있으면 어떨까??

Multi Layer Perceptron(MLP)

• 위의 Motivation에도 말했지만, 한 개의 퍼셉트론으로는 많은 문제를 처리하기 힘듦.

• 즉, 여러 개의 퍼셉트론을 활용할 이유가 있고, 이 때문에 Multi-Layer Perceptron이 고안됨

• MLP는 앞으로 진행되는 Feed-Forward artifical neural network이다.

• 구조로는 1. Input Layer 2. Serveral hidden layer 3. output layer로 구성 되어 있다.

• 이때, Layer과 Layer 사이에 있는 것들을 node라고 칭하고 이전의 Layer이 새로운 Input, 다음 Layer의 각 요소(Node라고 칭함)들이 output이 되고, 이것들을 이루는 것이 하나의 perceptron이 된다.

• 즉, 두번째 Layer가 만약 $\R^{k}$라면 이는 $k$개의 퍼셉트론이 존재하는 것으로 보는 것!

• Output Layer를 제외한 모든 Layer에는 반드시 Non-linear activation function을 거쳐야하며(안거치면 큰 의미가 없음) 마지막에서는 상황에 따라 Softmax function을 거치게 된다.

Deep Neural Network & Why use deep network?

• 앞에서 소개했던 것은 사실 딥러닝에서 학습을 하는 구조 중 하나
  • 이외에도 CNN(Convolution Neural Network), RNN(Recursive Neural Network), LSTM(Long short term Memory), GNN(Graph Neural Network) 등 굉장히 많은 종류가 있다.
  • 가장 기본적인 꼴이며, 앞으로 진행되는(순서가 있는) Feed-Forward의 대표 네트워크 격임

• 특히, 그 중에서도 Hidden Layer가 굉장히 많으면 많을수록 좋다(그렇다고 Node들이 적으면 또 크게 좋진 않음)

• 왜 좋은지에 대해 알아보자.
  1. Output을 낼 때 많은 Feature들이 개입된다.
     • 한 Layer를 거쳐갈 때마다 이전 Layer의 Weighted sum을 한 이후 Activation Function을 거쳐가게 됨
     • 즉, 이전 레이어들의 정보를 모아 새로운 특징(Feature)을 찾아내는 일련의 과정이라고 볼 수 있음
     • 만약 Layer들이 많으면 많을수록 더 질이 높은 정보를 뽑아낼 것이고, 그러면 더 좋은 모델이 됨
     • 다만, Layer들이 너무 많으면 추후에 나오겠지만 너무 Traning data에 치중되어 있는 Overfitting Problem을 야기할 수도 있음
  2. 첫 Input들이 마지막 Output Layer로 갈 때 경우의 수가 많아짐
     • E.g. 다음 그림을 보자

     

     [출처] https://jjeongil.tistory.com/535

     • 다음 그림을 보면, Input 1이 Property 1로 갈 때 거쳐가는 수는 Hidden Layer의 Node 수인 3이다. 이러한 계층이 2개, 3개, .. $n$개가 되면 Layer 당 Node수가 3이기만 해도 총 $3^n$개가 됨을 알 수 있다.

• 이러한 DNN에서 우리는 보통 1. Forward Pass를 통해 값을 계산하고, 2. Backpropagation을 통해 Weight들을 갱신한다.

• Backpropagation을 하기 전에 먼저 Forward Pass를 알아보자.

• Forward Pass는 아주 간단한 계산이다. 다음 그림을 보자. (그림의 명칭을 그대로 활용한다.)

[출처] https://stackoverflow.com/questions/63331975/what-is-the-preferred-mathematical-representation-for-a-forward-pass-in-a-neural

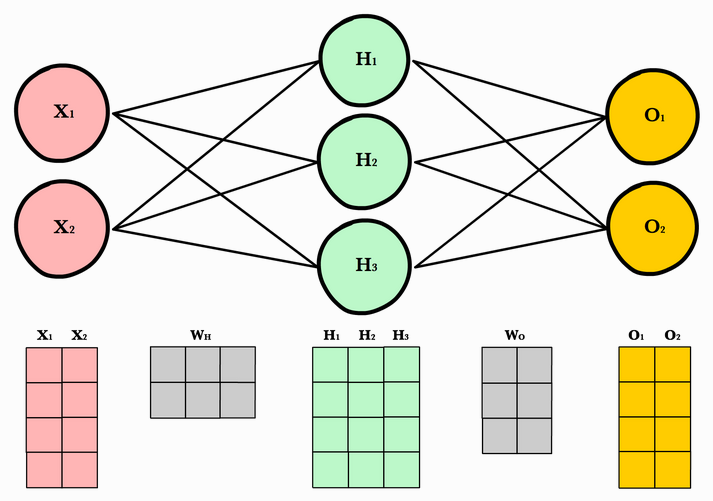
• Weight들에 대해 보이지는 않지만, $W_{ij}^K$를 $K$번째 Layer의 $i$번쨰 노드가 $K+1$번째 Layer의 $i+1$번째 노드로 갈 때의 weight 값이라고 하자.

• 그러면, $H_1$이 계산되기 위해서는 $\sigma(W^1_{11}x_1+W^1_{21}x_2)$를 해야 함을 알 수 있다.

• 이를 내적의 관점에서 보면, $\begin{bmatrix}W_1\ W_2\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}$이라고 적을 수 있고, 이러한 Weight vector들을 층층히 쌓는다고 생각하면, Weight들만 모은 Matrix를 생각할 수 있다. $K$번째 Layer들에서의 weight Matrix을 $W_K$라 하자. 세로 행은 직전 Layer들의 모든 Node 하나의 Output으로 갈때의 Weight들을, 가로 열은 직전 Layer Node 하나가 각 output으로 갈 때의 Weight들을 의미한다.

• 그러면 계산을 $W_kx+b_k$($b_k$는 편항)으로 간단하게 계산할 수 있고, 이후 Activation Function을 거쳐 계산된다.

Appendix

• 이번 장에서는 왜 우리가 Activation function을 사용해야 하는가에 대해 알아볼 예정이다.

• 일단 먼저 Layer $i$에서 $i+1$로 갈 때의 가중치의 모임을 $W_i$라 하자.

• Input Layer가 $i=1$이며 Output Layer는 $i=k$라고 한다.

• Input으로는 $\mathbf{x}$를 활용하고, Activation function은 $\sigma(z)$를 활용하도록 한다.

• 그러면, Layer들에 대해 Feed-Forward를 진행하면

$$\hat{y}=\sigma(W_k\ \sigma(W_{k-1}\cdots\sigma(W_2\ \sigma(W_1\mathbf{x}+b_1)+b_2)+\cdots+b_{k-1})+b_{k})$$

가 됨을 알 수 있다.

이때, 만약 Activation Function이 활용되지 않으면 식이

$$\hat{y}=W_k(W_{k-1}\cdots(W_2(W_1\mathbf{x}+b_1)+b_2)\cdots+b_{k-1})+b_k$$

가 됨을 알 수 있다.

이때, $W_i$들은 단순한 행렬이므로 행렬 곱을 할 수 있고, 행렬곱을 통해 새로운 행렬을 만들어낼 수 있다. 같은 방법으로 편향에 대해서도 Matrix와 Vector의 Operation을 시행하면 동일하게 새로운 편향이 나오고, 이는 하나의 퍼셉트론이 내는 결과와 동일하게 된다! ⇒ 의미가 퇴색됨

Uploaded by N2T