5. Backpropagation

Motivation

• 앞에서 MLP와 Forward Pass를 통해 예측값을 계산하였고, SGD를 통해 이 예측값을 통하여 어떻게 파라미터를 조정하였는지 배웠다.

• 그러면, 언제 이 파라미터를 조정할 것인가? 또한, 어떻게 조정할 것인가?

• 이에 대해 연산을 하는 것이 backpropagation이며, activation function으로 sigmoid나 ReLU와 같은 함수가 택된 이유에 대해 알아보자.

Backpropagation

• 한 Iteration이 끝날 때 예측 값과 실제 값의 차이를 합친 cost를 기반으로 가중치를 역으로 진행하면서 업데이트 하는 과정

• 즉, Forward Pass에서는 Layer 1에서 끝($k$)까지 진행하였다면 Backpropagation은 $k$에서 1로 진행한다고 생각하면 된다.

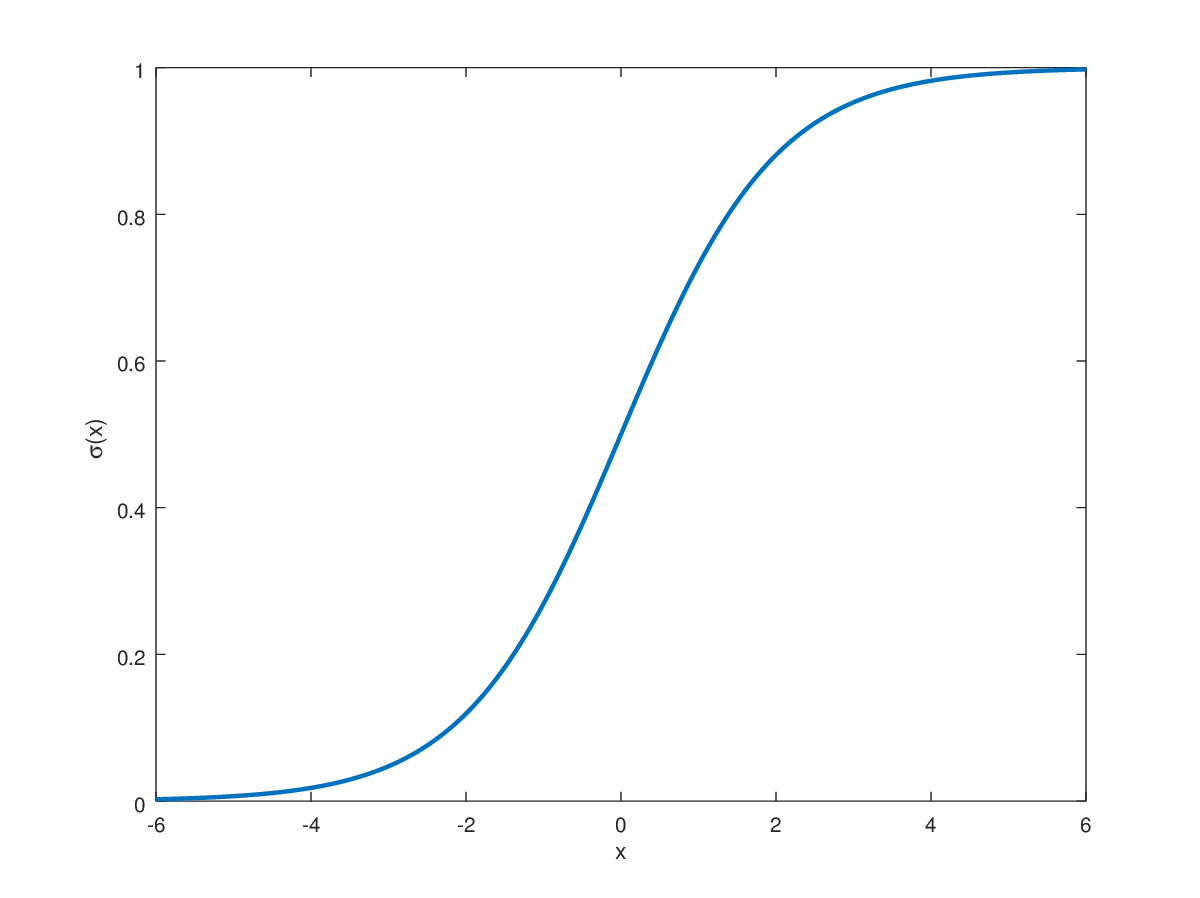
• 먼저 sigmoid-function의 특징에 대해 알아보자.

Sigmoid Function (1)- derivative

• 시그모이드 함수 같은 경우 여러 가지 특징이 있고 이에 따라 일어나는 문제점도 많지만 지금은 Backpropagation에서 사용되는 특징만 알아보도록 하자.

• sigmoid function을 다시 작성해보자

$$f(z)=\dfrac{1}{1+e^{-z}}$$

• 몫의 미분법을 활용하여 미분하면

$$f'(z)=-\dfrac{-e^{-z}}{(1+e^{-z})^2}=\dfrac{e^{-z}}{(1+e^{-z})^2}$$

• 이때 $f(z)=\dfrac{1}{1+e^{-z}}$이므로 $1-f(z)=\dfrac{e^{-z}}{1+e^{-z}}$이고, 따라서

$$f'(z)=\dfrac{e^{-z}}{1+e^{-z}}\times\dfrac{1}{1+e^{-z}}=f(z)\{1-f(z)\}$$

• 실제로 컴퓨터가 어떠한 함수를 미분하는 것은 굉장히 자원이 많이 든다. 한 두개의 함수에 대해서 하는 것은 괜찮을 지 모르겠으나, 학습해야하는(계산해야하는) 파라미터가 수십 수백만개가 있는 딥러닝에서는 함수를 직접 미분하는 것은 거의 자살행위에 가깝고, 간단한 연산들로만으로 미분을 한 듯한 효과를 낼 필요가 있다. ⇒ 미분을 한 값이 원래 값과 1에서 그 값을 뺸 것의 곱은 단순한 사칙연산이므로 가능!

• 추가적으로 ReLU에서는 이 값이 $1$ 또는 $0$으로 고정이 되기 때문에 간단히 계산이 된다.

[출처] https://hvidberrrg.github.io/deep_learning/activation_functions/sigmoid_function_and_derivative.html

• 추가로 여러 가지 activation function에 대해서는 6장에서 알아볼 예정

Back to propagation... How can I do it?

[출처] https://d2l.ai/chapter_recurrent-neural-networks/bptt.html

• 앞에서도 지속적으로 언급했다시피 Backpropagation은 최고의 optimal parameter들을 찾는 것이고, 이는 Cost를 점점 줄여나가는 방향으로 진행해야함

• 즉, Cost의 Gradient를 이용하여 Gradient descent를 진행한다는 뜻이고, 이 과정에서 너무 많이 업데이트 되어서 값이 튀는 것을 방지하기 위해 learning rate를 설정한다고 하였음.

• 식으로 나타내면

$$w_i(t+1)=w_i-\eta\dfrac{\partial C^t(\theta)}{\partial w_i}$$

• 의미를 알아보면 Cost C에서 $w_i$가 영향을 미치는 모든 항들에 대해 gradient descent를 진행한다로 파악할 수 있다. 이 의미를 반드시 기억하고, 본격적인 식을 찾아보자.

Perceptron Backpropagation($1$ Layer)

[출처] https://ds-uno-blog.netlify.app/2020/06/04/backpropagation-neural-network/

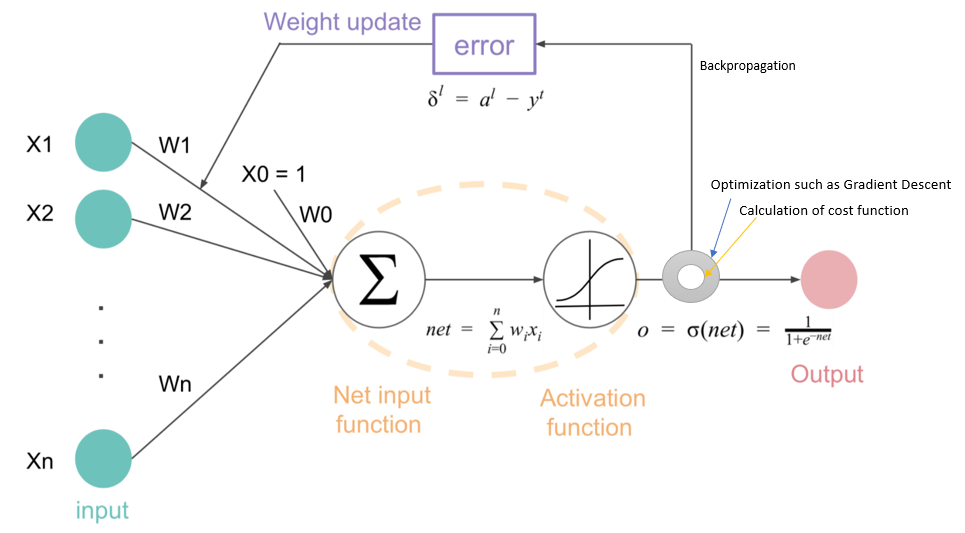
• 일단 퍼셉트론에 대해 역전파가 어떻게 이루어지는지 살펴보자. 이번엔 $w_i$에 대해 알아보도록 하겠다.

• 일단 앞의 식을 통해 우리는 업데이트를 위해서는 $C^t(\theta)$에서 $w_i$에 대해 미분한 값, 즉 $\dfrac{\partial C^t(\theta)}{\partial w_i}$이 필요하다.

• 하지만, 잘 생각해보면 $w_i$가 바로 $C^t(\theta)$로 가는 것이 아니라, weighted sum을 한 이후 activation function을 거치고, 마지막으로 Cost로 들어가게 된다.

• Weighted sum을 한 값을 $z$, Activation function(Sigmoid)를 거친 값을 $\hat{y}$라 하자.

• 그러면, $w_i$는 $z$를 연산하는데 직접적으로 영향을 끼치고, $z$는 $\hat{y}$에, $\hat{y}$는 $C^t(\theta)$에 영향을 미침을 알 수 있다.

• 이때 $z=\sum_{i=1}^k w_ix_i$이므로 $\dfrac{\partial z}{\partial w_i}=x_i$, $\dfrac{\partial \hat{y}}{\partial z}=\hat{y}(1-\hat{y})$, $\dfrac{\partial C}{\partial \hat{y}}=(\hat{y}-y)$이다.

• Chain rule에 의해, 우리가 구하고자 하는 $\dfrac{\partial C^t(\theta)}{\partial w_i}$은

$$\dfrac{\partial z}{\partial w_i}\dfrac{\partial \hat{y}}{\partial{z}}\dfrac{\partial C}{\partial \hat{y}}=x_i\hat{y}(1-\hat{y})(\hat{y}-y)$$

로 적을 수 있다. 이때, $\hat{y}$는 output value, $y$는 우리가 알고 있는 answer value, $x_i$는 input value임을 감안하면 오직 우리가 알고 있는 값들의 사칙연산만으로 그래디언트를 만들 수 있다!

Multilayer Backpropagation

• 다만, 우리는 Multi layer의 세계에 살고 있으니.., 멀티레이어에서는 어떻게 되는지 알아보자.

• 앞에서도 말했듯이 Multilayer는 결국 퍼셉트론의 중첩이다. 퍼셉트론이 모이고 모여서 다음 레이어로 점진적으로 뻗어나가는 방식이기 때문에, 기본적인 계산과정 등은 모두 동일하다.

• 다만, 퍼셉트론에서는 Cost로 바로 항이 넘어갔다면, 멀티레이어에서는 Cost로 바로 가지 않고 다음 Layer로 가기 때문에 중간에 식이 추가됨을 기억하라.

[출처] http://neuralnetworksanddeeplearning.com/chap2.html

Layer 1의 $i$번째 노드가 Layer 2의 $j$번째 노드로 갈 때의 weight를 $w^1_{ij}$라 하자. 그러면, Propagation 식은

$$\dfrac{\partial C}{\partial w_{ij}}=\dfrac{\partial z_1}{\partial w_{ij}}\dfrac{\partial{\hat{y}_1}}{\partial z_1}\dfrac{\partial C}{\partial{\hat{y}_1}}$$

가 된다.

• 여기서, 생각해보면 Cost $C$와 $\hat{y}_1$은 큰 관련이 없고 $\hat{y}_1$은 다음 layer $3$의 노드들에 연결되어 있는 weight들에 영향이 있다. 즉,

$$\dfrac{\partial{C}}{\partial \hat{y}_1}=\sum_k w_{jk}\dfrac{\partial \hat{y}_2}{\partial z_2}\dfrac{\partial C}{\partial \hat{y}_2}$$

• $\hat{y}_2$도 동일하게 chaine rule로 전개할 수 있고, 중간의 $\dfrac{\partial \hat{y}_2}{\partial z_2}$는 sigmoid function의 성질에 의해 쉽게 연산이 가능하므로, 식은 조금 복잡해져도 결국은 간단한 사칙연산으로 다 처리할 수 있음을 알 수 있다.

Vanishing Gradient

• 다시 sigmoid function의 미분꼴을 보면, $f'(z)=f(z)\{1-f(z)\}$이고, 만약 $f(z)$가 $0$이나 $1$에 가까운 값이면, $f'(z)\rightarrow 0$이 된다. 즉, Backpropagation 과정에서 거의 $0$에 가까워지고, 더하기가 아니라 전부 곱하기가 이루어지는 Back prop 과정임을 생각해보면 weight가 학습되지 않고 같은 값으로 유지되는 결과가 일어난다.

• 즉, 역순으로 진행이 되며 값이 점점 작아지고, 이 때문에 코스트의 값이 의미가 잃어버리는 경우가 생긴다.

• 이는 파라미터를 업데이트 해가면서 최적의 가중치를 찾아가는 딥러닝의 의미에 크게 위반된다.

• 이러한 상황을 고치기 위해 ReLU activation function이 제시되었다.

Uploaded by N2T