6. Universal Approximation Theorem

Cybenko Theorem

• Neural Network의 한계란 없다를 수학적으로 보여주는 정리

• 아래에서 사용하는 모든 함수는 sigmoid function을 기반으로 함을 기억하자.

• 구간 $\left[0,~1\right]^n$에서 countinuous한 임의의 함수 $F$와 양수 $\varepsilon$에 대해 항상 $F(x)$와의 차이가 $\varepsilon$보다 작은 neural network을 만들 수 있다.

• 간단하게 말하면, 아무 연속함수를 들고와도 단 하나의 Hidden Layer만 있으면 얼마든지 근사할 수 있다라는 것이다.

• $\varepsilon$이 굉장히 작으면 어떻게 그게 될지 의문이 들겠지만, 적분과 비슷한 테크닉을 기반으로 Hidden Layer의 Node수를 늘리면 그것이 가능하다! 이제 살펴보자.

Step function

• 우리가 적분을 증명할 때를 생각해보면 중점에 대해(Or 양 끝점) 직사각형을 만들고, 그 간격을 굉장히 좁게 하여 오차를 줄이는 방법이다.

• 자세한 리만 적분해서는 Analysis에 수강하니 넘어가도록 하고, Cybenko Theorem도 동일하게 이 기법을 활용한다.

• 그러기 위해서는 일정 구간에서만 값을 가지는 함수가 필요한데, 이 함수를 만들기 위해 Step function이란 것을 생각해보자.

• Step function은 특정 지점을 기준으로 값이 일정한 값으로 바뀌는 함수를 의미한다. 계단함수라고도 한다.

[출처] https://commons.wikimedia.org/wiki/File:Step_function.svg

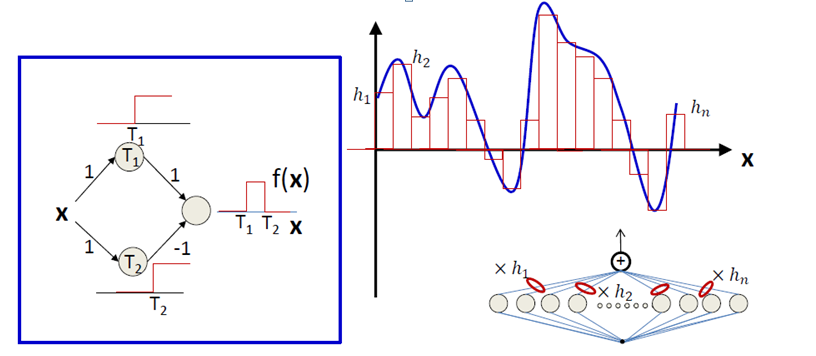
• 그러면, 이러한 Step function을 두 개 섞으면 어떻게 될까? 값은 같은데 1) 어디에서 step이 걸리는지 2) 방향이 어떻게 되는지에 따라 값이 0이 될수도, 이외의 값이 될 수도 있다.

• 이제 우리의 목표는 sigmoid function을 step function으로 근사하는 방법이다. 이것만 근사할 수 있으면 step function과 weight들을 적절하게 잘 취해줌으로써 일정 부분에서만 값을 가지는 것으로 함수로 바꿀 수 있다.

Approximation sigmoid function to step function

• $\sigma(z)=\dfrac{1}{1+e^{-z}}$에서 $\sigma(az+b)=\dfrac{1}{1+e^{-az-b}}=\dfrac{1}{1+e^{-a\left(z+\dfrac{b}{a}\right)}}$로 쓸 수 있고, 이는 시그모이드 함수를 $-\dfrac{b}{a}$만큼 평행이동하고 $a$만큼 scaling을 한 것이라고 볼 수 있다.

• 즉, 우리가 $0.4$ 지점에서 step function을 만들고 싶으면 $-\dfrac{b}{a}=0.4$ 로 설정하고, Step function이므로 scaling을 무한대, $a\rightarrow \infty$로 만들면 Step function과 아주 가깝게 된다(근사)

[출처] http://neuralnetworksanddeeplearning.com/chap4.html

이를 이용하여 Hidden node수를 늘리면 approximation을 할 수 있다.

[출처] https://medium.com/analytics-vidhya/neural-networks-and-the-universal-approximation-theorem-e5c387982eed

Uploaded by N2T