7. Softmax & Loss (1)

What is softmax?

• Softmax layer란 classification이나 regression 등에서 마지막에 output layer에서 확률과 비슷한 성질을 가지게 처리해주는 부분

• Softmax layer에서 사용하는 함수를 Softmax function이라 하고, 추후 편의를 위해 output layer 직전까지의 결과를 $\mathbf{x}=[x_1,~x_2,~\cdots,~x_n]^T$, 즉 $\mathbf{x}\in\R^n$이라 하자.

• 이때 softmax function $f(\mathbf{x})\ :\ \R^n\rightarrow\R^n$에 대해 다음과 같이 정의한다.

$$f(\mathbf{x})=\begin{bmatrix} \dfrac{exp(x_1)}{\sum_{i=1}^n exp(x_i)}\\\\ \dfrac{exp(x_2)}{\sum_{i=1}^n exp(x_i)}\\\\ \vdots\\\\ \dfrac{exp(x_n)}{\sum_{i=1}^n exp(x_i)}\end{bmatrix}$$

• 이때 $exp(x)$는 자연상수를 밑으로 하는 지수함수를 의미한다.

• 이가 확률과 비슷한 성질을 가지고 있다고 했는데, 왜 그렇게 되는지 확인해보자.

• 확률 같은 경우
  1. 총 합이 1이여야 하며
  2. 모든 값이 0보다 크거나 같아야 하고,
  3. 발생할 수 있는 event 수가 많을 수록 높은 확률값을 가지고 있어야 한다.

• 물론.. 확률 자체도 정의하기 위해서는 Measure라는 다른 개념을 들고 와야하지만, 너무 deep하니까 이건 빼고 알아보도록 하자.
  1. $\hat{y}=f(\mathbf{x})$라 하면 $\displaystyle\sum_{i=1}^n \hat{y}_i=\displaystyle\sum_{i=1}^n \dfrac{exp(x_i)}{\sum_{j=1}^n exp(x_j)}=1$ (분모가 상수이기 때문에 앞으로 빼고 계산)
  2. $exp(x)>0$이기 때문에 trivial
  3. 이를 보이기 위해 $\exist ~i,\ j\leq n\ :\ x_i>x_j$라 하자.
     • 이때, $h(x)=exp(x)$라 하면 $h'(x)=exp(x)$이므로 $\forall x\ :\ h'(x)>0$, 즉 $h(x)$는 증가함수이다.
     • 앞에서도 말했다시피 분모는 상수이므로 분자가 크면 클수록 더 큰 값을 가지고, 따라서 $\hat{y}_i>\hat{y}_j$이다.

• 하지만, 식을 보면 알 수 있듯이, 이는 확률이랑은 엄연히 다른 개념이다.

• 우리가 필요한 것은 어떠한 값이 얼마나 많이 나올지, 즉 확률에 대한 값이 필요한데 왜 흔히 아는 정의를 사용하지 않고 이렇게 복잡하게 softmax를 활용하여 계산을 할까?

Why softmax? (1) - probability & gradient aspect

• 앞에서 수도 없이 언급했듯이, softmax function은 probability 관점에서 바라볼 수 있기 때문에, 확률을 대신하는 개념으로 자주 사용된다.

• 다만, 일반적인 확률 대신 선택 받은 이유는 범용성 때문이다.

• 생각보다, 일반 확률은 불편한 점이 많다. 만약, 모든 $x_i$의 값이 $0$보다 크다면 상관이 없지만, $x_i$가 음수가 되는 순간부터 헬파티이다.

• 이를 막기 위해 절댓값을 취해주면, 그 때부터는 미분 여부에 대해 문제점이 생긴다!

• 일반적으로, 우리는 절댓값 함수가 미분이 가능하지 않다고 배웠고, 뭐 다변수 함수가 된다고 그러한 점이 크게 변하지는 않는다. 실제로 다변수함수에 대한 미분을 그래디언트라고 하는데, 그래디언트를 계산하는 방법도 우리가 일반적으로 미분하는 방법과 크게 다르지는 않다. (편미분)

• 우리는 단순히 모델에 대한 학습 정도를 파악하는 것이 아니라, parameter들을 직접 학습해야한다! 이러한 과정을 이전에 Backpropagation이라고 하였다.

• 이때, 앞에서도 말했듯이 계산해야하는 양이 굉장히 많기 때문에 backpropagation에서 계산하는 미분값은 사칙연산을 통해서 모두 계산이 되어야하고, 사칙연산이든 말든 기본적으로는 미분이 되어야 한다!

• 하지만, 절댓값 함수 자체가 미분이 불가능하기 때문에, 그것들 자체가 미분이 가능하다는 보장이 없다.
  • 물론, sigmoid function 등을 1회 걸쳐서 확률로 만든 다음 계산하는 방법도 있을 수 있으나, 그렇게 할 바엔 든든하고 뜨끈한 softmax 한번 조지고 만다 (물론 sigmoid 자체가 softmax function에서 n=2인 경우라서.. 두 개는 굉장히 유사하다)

• 이 뿐만 아니라, softmax는 Invariant 특성을 가지고 있다.
  • Invarinat는 불변의 라는 의미인데, 보통 Invariant under X라고 하면 X에 대해 변하지 않는 것을 의미한다. 예를 들어, 함수 $f$가 scaling에 invariant하다면 $f(cx)=f(x)$의 특성을 가지고 있다.
  • softmax는 Scaling에 대해서는 Invariant하지는 않고, translation에 대해 invariant하다. 즉, $f(x+c)=f(x)$이다.
  • 이 말인 즉슨, 확률 분포의 값이 단체로 여러 칸 이동해도 크게 변하지 않음을 의미한다.
    • 참고로, 일반적인 확률 개념에서는 변한다. 만약 $N$개에 대해 $c$만큼 움직이면 분모가 $cN$만큼 커지므로, 영향력이 전체적으로 변하게 된다.
  • 이 덕분에, 값의 크기가 아니라 값들이 어떠한 분포를 가지고 있느냐에 따라 softmax 값이 정해진다는 큰 장점이 있다.

Why Softmax? (2) - Information aspect

• 다음은 정보 이론에서 다루는 내용과 큰 관련이 있다.

• 간단하게 요점부터 말하면, Backpropagation 과정에서 gradient를 계산할 때, probability distribution으로 softmax를 활용하게 되면 굉장히 간단하게 결과가 나온다.
  • 그래디언트의 값이 $\hat{y}-y$가 되는데, 일단 이걸 자세하게 설명하기 위해 여러 가지 사실을 알아보자.

Likelihood

• 번역하면 “가능도”라고 불리는 요소인데, 뭐가 가능하단 것인지 한번 보자.

• 우리는 일반적으로 어떠한 확률 분포가 주어졌을 떄, 어떤 이벤트가 발생하는 것을 확률이라고 한다. 이를, 조건부 확률을 사용하여 표시하면
  • distribution을 이룰 때 사용한 parameter를 $\theta$, event는 $x$이다.
  • 이때, 확률 $P$는 $P(x\ |\ \theta)=P_\theta(X=x)$라고 적을 수 있다.

• 하지만, 우리는 일반적으로 “어떠한 값”에 대해서는 알기 쉬우나, “어떠한 분포”인지는 알기가 굉장히 어렵다. DL이나 ML에서는 이것을 간략하게 approximation 하기도 하고…

• 따라서, 우리는 역으로 어떠한 값이 주어졌을 때 이 값이 해당 distribution에서 나왔을 확률이 얼마인가?에 대해서 알아볼 필요가 있다. 즉, 이때까지 $y=f(x)$에 대해서 탐구했다면 지금은 $x=f^{-1}(y)$에 대해서 탐구하는 느낌이라고 보면 될 듯 하다.

[출처]: https://dlearner.tistory.com/43

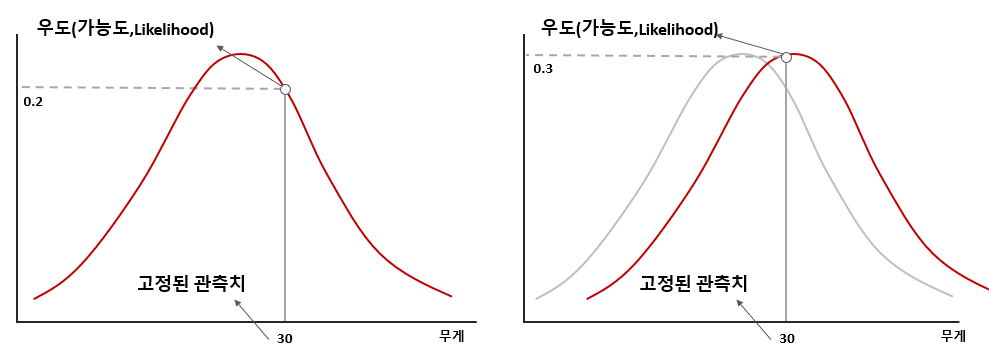
• 이를 “가능도”라고 하고, 동일하게 $x$와 $\theta$라 하면 $\mathcal{L}(\theta\ |\ x)$라고 적는다.
  • 아주 자주 쓰는 예시로(다른말로 위키피디아 펌이라는 뜻 ㅎ)
    • 만약 아주 이상적인 동전을 던진다고 하면, 앞면이 나올 확률은 $0.5$이다.
    • 앞면을 $\mathrm{H}$라 하고, 동전을 $\theta$라 하면 $P(\mathrm{HH}\ |\ \theta)=0.25$가 된다.
    • 역으로, $P(\theta\ |\ \mathrm{HH})$에 대해서 알아보면, 이미 동전이 앞이 두개가 나온 상황에서 앞면이 나올 확률을 $0.5$라고 하자.
    • 그러면, 앞면 두개가 나올 확률은 당연히 $0.25$이다.
    • 즉, 확률에서는 distribution을 고정하고 event들을 요리조리 움직였다면, 가능도에서는 역으로 event를 고정하고 distribution을 요리조리 옮기는 것이다.

• 말했다시피, 우리가 알고 싶은 것은 어떠한 parameter들일 때 이러한 관측값들이 최대가 되는가?이다. 이를 Maximum likelihood estimation(최대우도법)이라고 한다.
  • 자세하게는 2탄에서 KL-divergence와 함께 다룰 예정이다.

Entropy

• 이제 잠시 주제를 바꾸어서, Information theory으로 넘어가보려고 한다.

• Entropy는 물리에서 자주 나오는 개념이라 열역학 쫌 쳐봤다 싶으면 익숙한 개념일텐데, 비슷하다.
  • 일반적으로 Entropy는 “무질서도”라는 의미를 가지고 있는데, 다른 말로 하면 “불확실성”을 의미한다.
  • 만약 질서정연하게 있으면 어떠한 객체가 어디쯤 있을지는 쉽게 예측할 수 있다. 서있는 곳 찍으면 되니까.. 하지만, 여러 가지로 퍼져 있으면, 그걸 찾는것은 기하급수적으로 어려워진다.
  • 왜y? 공간이 넓어지고 그러면, 어떠한 자리에 있을 “확률”이 낮아지기 때문
  • 즉, Entropy는 확률이랑 아주 밀접한 관련이 있으며, 확률이 낮으면 낮을수록 그 정보에 대해서 확신을 할 수 없게 된다. 이럴 때 우리는 “엔트로피가 높다”라고 한다.

• 조금 더 엄밀하게 말하면, 엔트로피는 어떠한 정보(확률)에 대해 이것이 일어나면 얻을 수 있는 정보량이라고 생각하면 좋다.

• 예를 들어, 일이 99%로 일어난다고 치자. 만약 그 일이 일어나면, 우리는 “아~ 익숙하구머잉”이라고 하면서 넘어가지 와 킹갓세계엠퍼럴망햇다세계멸망의대징조가보인다우리의인생은어떻게하지 이런 스탠스를 보이지 않는다.

• 즉, 너무 자주 일어나기 때문에 그 일이 일어나도 얻을 수 있는 정보가 많이 없다.

• 하지만, 갑자기 내가 로또 당첨되면 천재일우의 기회라면서 떠받혀준다. 확률이 극히 적으니, 이런 일이 일어나면 뭐 어떤 꿈을 꿨느니 어떤 루트로 길을 걸었느니 주변에서 별 시덥잖은 거 다 물어보지 않는가? 비슷하다. 아주 드문 일이 일어나면 그 일이 일어난 경위 등에 대해서 정보를 얻을 수 있게 되고, 이런 것을 보고 정보량이 많다라고 한다.

• 즉, 확률이 낮으면 낮을 수록 정보량이 높음을 알 수 있고, 이것의 기댓값을 엔트로피라고 하자는 것이다.

[출처]: https://en.wikipedia.org/wiki/Entropy_(information_theory)

• 그러면 우리는 이 정보량이라는 정량적으로 표현할 방법이 필요하다. 간단하게 생각해보자.

• 우리는 일반적으로 정보를 얻는다라고 생각을 할 때, 어떤가가 참인가? 거짓인가?로 판단하게 된다. 즉, 어떠한 가정을 세우고 그에 대한 답을 듣고 그걸 정보로 삼는 것이다.

• 이제 한 가지 집합을 정의하자. 총 $16$개의 공이 있는데, $8$개는 빨강, $4$개는 노랑, 흰색과 검은색 공은 $2$개씩 있다고 하자.

• 친구가 공 $1$개를 뽑고, 우리한테 어떠한 색인 것 같냐고 물어본다. 이 경우, 차례대로 빨간색 공? ⇒ 노란색 공? ⇒ 흰색 (or 검은색) 공? 의 질문을 차례대로 던지면 된다.

• 즉, 빨간색 공일 확률은 $\dfrac{1}{2}$로 제일 높으므로 질문을 한번만 해도 알아낼 수 있고, 노란색은 $\dfrac{1}{4}$이므로 두번만 하면 알아낼 수 있다. 나머지 공은 $3$번은 해야한다.

• 즉, 우리는 하나의 사건에 대한 질문 수를 $\log \dfrac{1}{p(x)}=-\log p(x)$라고 할 수 있고, 기댓값(현재는 이산)은 $\displaystyle\sum_{\text{possible}~x} p(x)\times(-\log p(x))=-\sum p(x)\log p(x)$로 적을 수 있다.

• 이를 우리는 엔트로피라고 하고, $H$라고 보통 작성한다.

• 즉, 확률 벡터 $\mathbf{x}$에 대해 $H(\mathbf{x})=-\displaystyle\sum_{k=1}^n x_i\log(x_i)$로 정의한다.

• 현재 log로 자연상수를 썼는데, 이진로그를 써도 된다. 하지만.. 자연상수 쓰는게 일반적으로 편하므로 앞으로는 자연상수로 통일한다.

Uploaded by N2T